画像をダウンロード 連立方程式 3つ 行列 104749-連立方程式 3つ 行列

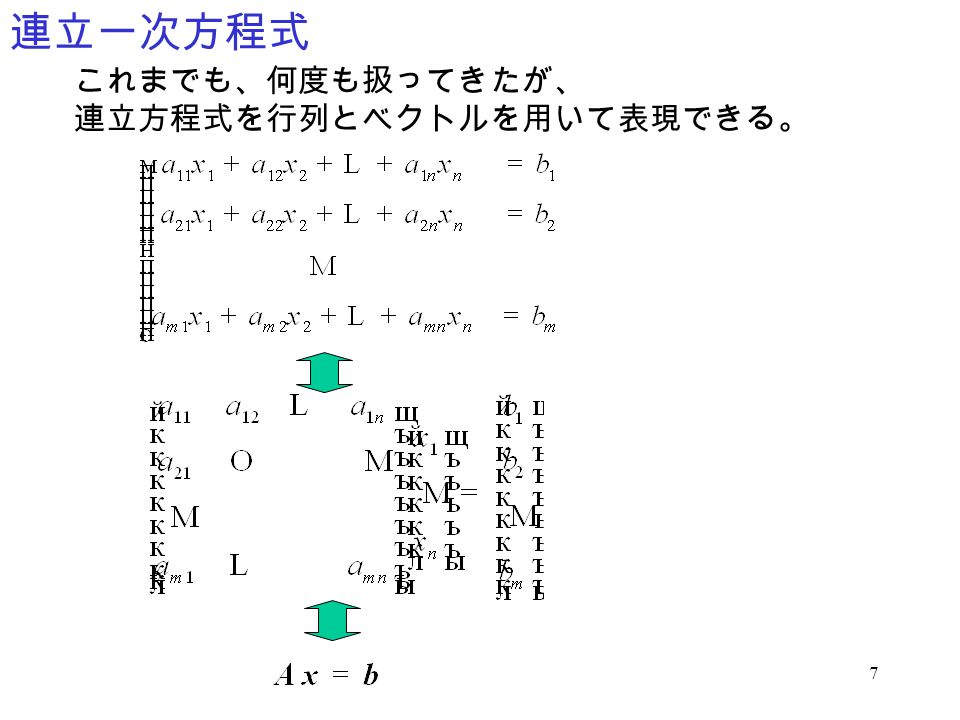
 今回は次の3元一次連立方程式を例として解説していきます。 2xy3z=6 x3y2z=1 3x2yz=7 正則行列であるか行列式を求めて確かめる 前回：二元一次連立方程式(「連立方程式を行列で解く方法(8）」)のときと同様に、まず行列の積の形であらわします。 式43 3は， ある行列に逆行列が存在すると言うことは， 行列で表現された方程式の解を求めることが出来ることを表しています。 ※1） inverse matrix ※2） regular ※3） regular matrix 連立一次方程式を行列の数学で解く 連立一次方程式は， 構造物の強度計算や流体のシミュレーション等， 科学技術計算に3元連立方程式の解を求めます。 \(\normalsize{\left\begin{array}\\ a_{\small 11}& a_{\small 12}& a_{\small 13}\\ a_{\small 21}& a_{\small 22}& a_{\small 23}\\a_{\small 31}& a_{\small 32}& a_{\small 33}\\\end{array}\right} {\left\begin{array}\\ x_{\small 1}\\ x_{\small 2}\\x_{\small 3}\\\end{array}\right}={\left\begin{array}\\ b_{\small 1}\\ b_{\small 2}\\b_{\small 3

1

連立方程式 3つ 行列

連立方程式 3つ 行列-連立1次方程式の一般的な解法として，消去法がある．消去法とは， （Ⅰ） 1つの方程式に0でない数をかける． （Ⅱ） 1つの方程式にある数をかけて，他の方程式に加える． （Ⅲ） 2つの方程式を入れ替える． の3つの演算をそれぞれ何回か行うことによって連立方程式の1つの式というのは，横に並んだ行だから，これを行列で書くと，次の3つの操作にまとめられる． これを 「行基本変形」 という． ⅰ) ある行を別の行と入れ替える．

三元連立方程式 ２ 中２数学 Youtube

これを連立 元 1 次方程式（simultaneous linear equations）という． 行列で書き直すと， (380) となる． 行列をそれぞれ文字で置き換えて (381) と表される． 行列により表現された方程式と元の連立 1 次方程式は等価な方程式である． のとき同次連立 1 次方程式または単に同次定義 38(連立 1 次方程式の基本変形) 連立 1 次方程式に対する次のの操作を連立 1 次方程式の基本変形と呼ぶ． (1) 一つの式を 倍する． (2) 二つの式を入れ替える． (3) 一つの式を 倍して別の行に加える． 連立 1 次方程式に基本変形をして得られた方程式と元の方程式とは等価な方程式である． すなわち両者は同じ解をもつ．行列式による解法は、未知数が3個ある三元の連立方程式に対しても適用することができる。三元の連立方程式について、これを示すと、 a 1 xb 1 yc 1 z=d 1 a 2 xb 2 yc 2 z=d 2 a 3 xb 3 yc 3 z=d 3

2 連立方程式の解は3パターンある 21 普通に解が出るパターン;連立一次方程式の解法と行列の行基本変形 連立一次方程式の加減法による解法を考察する。 ⎧23()(1) 37(2) xy xy ⎪⎪ = ⎪⎨ ⎪⎪ −= ⎪⎩ " " 式を減らすと、 逆方向の計算 (1) (2) ができない。 510x = 同値な変形ではない。 3例53 {xay = 0 xy = 0 (a は実数)を解こう． (1 a 1 1) −→ (1 a 0 1−a なので，a ̸= 1 のときは係数行列の簡約形はE2 になる．このときは x = y = 0 の自明な解しかない． a = 1 のときは係数行列のランクが1 になり，x = −y ならば何でも 解になる． 練習51 (教科書p33 問題23 (1), (4), (5)) 次の連立1 次方程式

簡約行列 掃き出し法により連立方程式の解を求めるとき, 拡大係数行列を簡約行列まで変 形する(行列を簡約化する) ことが重要である 定義33 (簡約行列) 次の条件を全て満たす行列を簡約行列という 1 零行があれば, 非零行よりも下に位置するが解をもつための定数a,b の条件を求めよ。 (2)次の連立1次方程式が解をもつようにkの値を定めて、その一般解を求めよ。 x1 3x2 − x3 =5 2x1 x2 3x3 =0 3x1 2x2 4x3 = k 解答1 解が存在する場合、検算は、得られた解が連立1次方程式を満たすか否かをチェッ作成者：黒田匡迪, 辻栄周平（監修：数学教室） 31 はじめに 「vol 1 行列の基本変形のやり方」において, 以下の3つの問題 問題1 連立一次方程式を解く問題 問題2 逆行列を求める問題 問題3 行列式を求める問題 は基本変形を繰り返し行うことで, 解くことが出来ると述べました

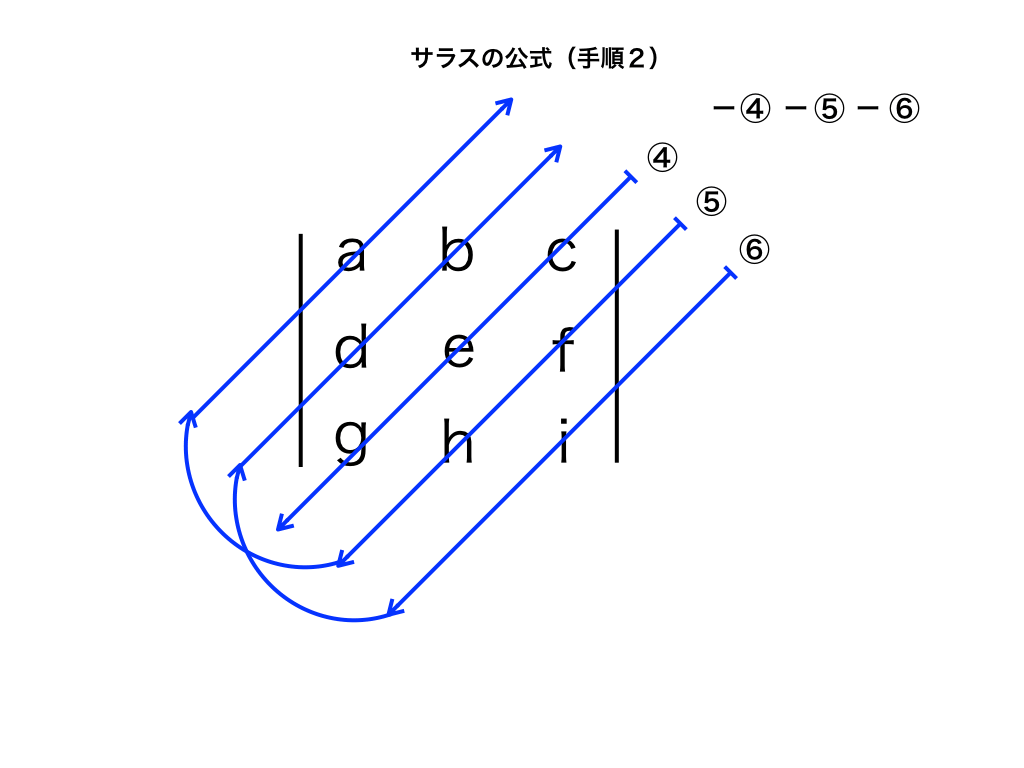
掃き出し法で連立方程式を解く手順とコツを解説

Excelで連立方程式を解く方法 Excelで統計解析

例3 次の連立1次方程式を考える。 3x1 − 2x2 x3 4x4 = 7 x1 − 3x3 x4 = 5 2x1 − x2 9x3 = 0 この連立1次方程式は、次の行列の方程式でも表される。X = (x y);(3) 1 つの行の定数倍を他の行に加える． という3 種類の変形を行列の行基本変形という． 行基本変形は可逆な変形である． 連立1 次方程式Ax = b の拡大係数行列(A b) が行基本変形により(A′ b′) に変形された とき，Ax = b とA′x = b′ は同じ解の集合をもつ． 階段行列(p72{74)

連立方程式の行列解

C 連立方程式解法 ガウスの消去法 Mk Mode Blog

講義の流れ 1 lu分解 lu分解 ピボット型lu分解 ピボット選択型lu分解 組み込み関数 2 コレスキー分解 3 連立一次方程式 4 まとめ 平井慎一(立命館大学ロボティクス学科) 数値計算：連立一次方程式 2 / 853 3行列式： 次に3変数連立1次方程式に対するクラメルの公式を作ってみよう。つまり解x;y;z を それぞれ行列式の比で書いてみたいのだが、もちろんそれには3 3 行列式を適切に定義する必要があ る。まず、連立1次方程式を 8 >< > a1xb1y c1z = p1 1 a2xb2y c2z = p2 2実数係数の連立一次方程式の行列を用いた解法を検証・実践する。 2 方針 数学Cの分野で学んだ行列を用いた二元一次連立方程式の解法を、n元連立一次方程式まで拡張す ることを目標とする。 そのために、以下の概念を順に検証する。 Ⅰ 解をもつ条件

簡約化と連立方程式 不定と不能 ぐるめも

第4回講義 基礎数学 数学入門

連立 次方程式 は、数値計算 を試みる人の前に頻繁に立ち現れる問題です。 方程式は = = で表記されます。未知数は = 個の です。 を行列形式で書けば = です。連立 次方程式の数値解法 とは、行列 とベクト ル に対し、 をみたす を数値的に求める方法 です。6x14y7x=27 6x14y7x=27を 整理してx14y=27 x14y=27の両辺に3をかけ、辺々たすと 3x10y = 23 ) 3x42y = 81 52y = 104 両辺を52で割るとy=2 y=2を3x10y=23に代入すると 3x=23 3x=3 x=1 1．行列で連立方程式を表すには 皆さんはこのような連立方程式の解き方を中学生のときに習ったはずです。 { 2 x − 3 y = − 5 − 3 x 4 y = 6 今回はこれを行列っぽく解いちゃいましょう。 まずは上の式を行列で書いてみます。 A = ( 2 − 3 − 3 4), x → = ( x y

３元連立１次方程式の解を持つ条件とその解 ３元連立１次方程式の解を 数学 教えて Goo

至急お願いします この連立方程式が解をもつように定数ｋを定 Yahoo 知恵袋

B = (8 5)2,090円（税込） 連立方程式から学ぶ行列・行列式 書影 「数学が得意とはいえない学生」や，高校で行列を習わずに大学に入学した学生へ向けた，行列と行列式の解説書。 主に，連立方程式と行列・行列式との関係を中心に展開している。 Σのような第三回連立方程式の解法 ガウスの消去法・行列 舟木剛 平成24年10月24日2限 数値解析‐3 1 シラバス • 授業の目的 – 工学分野でよく用いられる数値計算の算法ならびにそれらの数値的な特性について理解させる． • 授業計画 – 数値計算と誤差（1回）

第4回講義 基礎数学 数学入門

連立一次方程式を掃き出し法で解く6つの例題 理数アラカルト

3 行列と連立1 次方程式 (2 3 1 4)(x y) = (7 9) を満たすx;y を求める．左辺を計算すると， 2xy x 4y 7 9) となるので，これは連立方程式 {2xy = 7 x 4y = 9 と同値． 連立1 次方程式は行列を使って表現で連立一次方程式 {3xk=0,kx3y=0 がx=0,y=0以外の解を持つように定数kの値を求めてください。 また、この問題のように{3xk=0,kx3y=0の 3xk←yがない場合 どのように行列式を作ればいいのでこの例題の，(35)式の形に至るまで（すなわち，解がそれぞれ求まるまで）3つの演算を行う 解法を GaussJordan の消去法という．消去法は，変数の数が増えても有効な解法である． ところで，連立1次方程式(31)を行列の式で表すと

連立方程式の行列解

Intro Linear Note

線形代数学講義ノート まえがき これは大学1 年次を対象にした線形代数学の講義ノートである 前半部分では連立1 次方程式の解法 と行列式の計算を主に扱う 後半は線形空間の抽象論の初歩を踏まえた上で, 行列の対角化までを目標に 定めている連立方程式掃き出し法（不定，不能） 要点 連立1次方程式 は，行列を用いて， と書くことができます。 すなわち, A= ， X= ， P＝ とおくと， A X ＝ P となります。 方程式 は， （ア） Δ=ad－bc≠0のとき，ただ一つの解を持ち， X＝A 1 P となります。 （イ） Δ=adbc=0のとき，成分に分けて調べると i） (1)// (2)のとき 解なし ii) (1) (2)が一致するとき， 直線 (1)上の点 行列と連立方程式 次のような連立方程式を考えます。 3 x 1 2 x 2 = 11 2 x 1 − 5 x 2 = 1 この連立方程式は行列を使って次のように表現することができました。 ( 3 2 2 − 5) ( x 1 x 2) = ( 11 1) さあ、ではこの行列で表現した連立方程式を解いて x 1, x 2 を求めるにはどうすればいいでしょうか？ アイ 両辺を ( 3 2 2 − 5) で割れると、

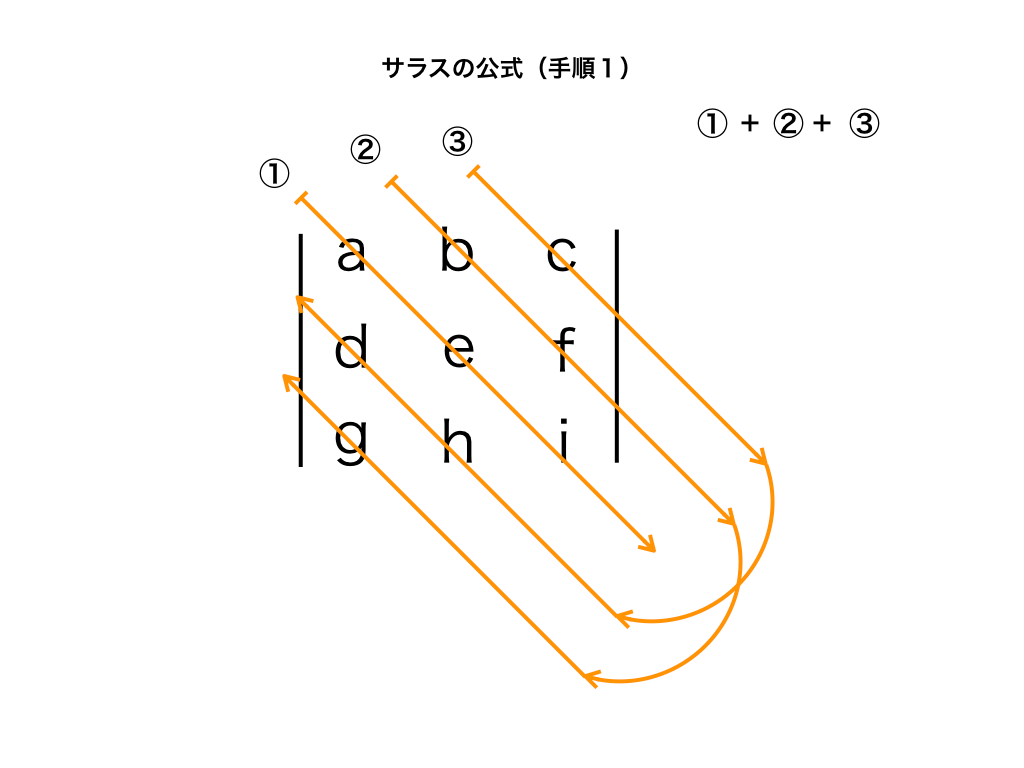
掃き出し法で連立方程式を解く手順とコツを解説

書記が数学やるだけ 44 逆行列を求める 2 余因子行列 行列のランク 連立方程式 3 クラメールの公式 鈴華書記 Note

作を施せば更に3行目以下は も消去された方程式系になる。この操作 を繰り返すことで最終的に # という3角行列による連立一次方程式に帰着できる。 # は行列が左下三角の行列が であることから第 成10 行列式1 決定する determine という動詞の派生語 determinant は，日本語では 行列式 と訳され，n次正方行列が正則であるか否かを判定できる式である．行列式の数学的な定義はこみいったものであるが，広く用いられる便利な式である． 以下において解説 行列式編連立方程式の解と行列式 試験対策線形代数の前期授業の要点が30分で分かるよう凝縮しました Clubhouse話題のSNSを始めた報告ジェネレーターを作った話（#5） 国会衆議院を傍聴する方法

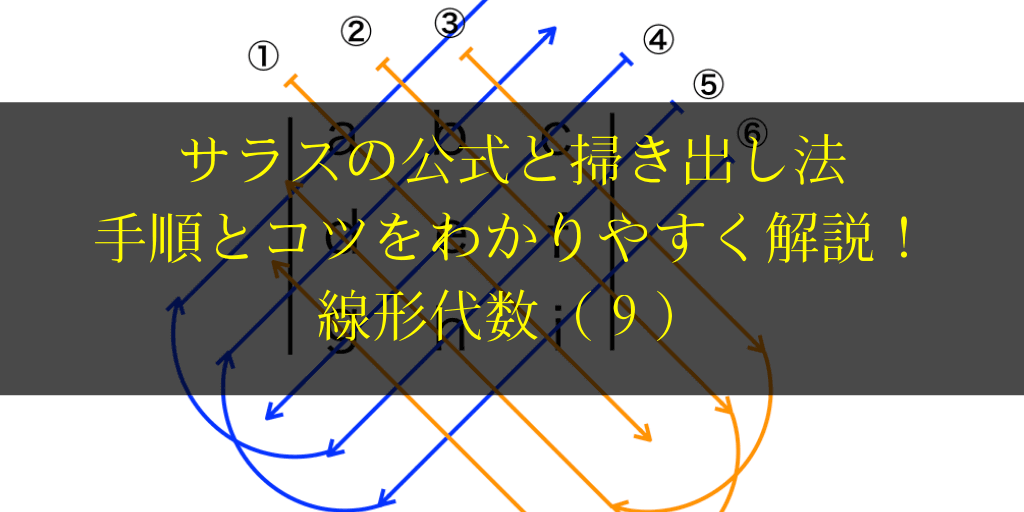
掃き出し法で連立方程式を解く手順とコツを解説

1

3 同次形の連立方程式 31 自明な解; 連立方程式を逆行列で解く手順 連立方程式を の形に変形 の逆行列を求める 両辺に の逆行列 を左側からかける 手順③についてですが、 これは と をかけると単位行列になるという逆行列の性質を使っています。 このように両辺に逆行列 をかけると左辺が の形になるので連立方程式の答えが求まるということですね！ ここで行列の方程式の は と の列ベクトル連立1次方程式には，無限個の解を持つものもある． (x y = 1 2x 2y = 2 この連立方程式で，変数消去をすると，第2式が消えて， xy=1 という式だけが残る．実際，この連立方程式には，本質的には一つの方 程式しかない．この方程式の解は，(x,y)=(1,0),(2,−1),(3

連立方程式の行列解

連立方程式の行列解

この場合、連立一次方程式を解くことは係数行列 の逆行列を求める問題に帰着される。 6 1 行列を使った連立一次方程式の表示(ベクトルと行列の積) 連立一次方程式は、第1節で説明したように、ベクトルと行列の積を使って表わされる。例 えば、連立一次方程式 {2x3y=8 x2y=5 は、 A = (2 3 1 2);まず、左から両辺に 逆行列 をかけます。 ここで、逆行列は以下のように計算されます。 この結果を使って行列方程式を解くと以下のようになります。 2X2行列の逆行列の計算 次に、 3X3行列 を使って 3 つの 未知数 を持つ 連立方程式 を解きます。 3X3行列の逆行列の計算 この場合も、左から 逆行列 をかけると、 行列式A は以下のように計算されます。 したがっExcel の行列計算による連立方程式の解き方 消去法との比較 例題 次の連立方程式を解きます。 解説 この方程式は、行列を使って、以下のように書けます。 ここで、 とおくと、方程式の解、x、y、z は、Aの逆行列を用いて のように、求められます。

基礎数学演習ｉ

逆行列で連立方程式を解く Aiコトハジメ

 行列を使って連立方程式を解く方法を紹介します。 計算例 3つの方程式 を行列であらわすと となります。この行列を逆行列を使って X、Y、Z に関して解くと となり連立方程式を行列で解くことができます。Z 5w = ¡3 が得られ, これは元の方程式と同じ解をもつ このとき, w に任意の値t を与えたとき, x, y, z はx = ¡4t ¡ 5, y = ¡1, z = ¡5t¡3 として, ただ1通りに定まるため, 元の連立方程式の解は, 8 >> >> >> < >> >> >> x = ¡4t¡5 y = 1 z = ¡5t¡3 w = t (t は任意定数) によって与えられる 1行列の除算 Octave には、「配列の左除算または右除算」と言う演算子があります。 / (mrdivide)、\ (mldivide) が使われます。 連立方程式や逆行列を考えずに、a・X = Y は、X = a \ Y として解けると言うことです。 この演算の答えは、擬似逆行列を掛けたものとは

５ 連立一次方程式 Ppt Video Online Download

次の連立方程式を逆行列を使って解いてください X Y 52x 3y Yahoo 知恵袋

 に対して、1列目、2列目を掃き出した結果は次のようになる。 3列目、4列目はこれ以上掃き出せない。 対応する方程式は、 \left\ { \begin {array} {l}x\phantom {y}3z\phantom {2}w=\phantom {}5\\\phantom {x}y2z2w=4\end {array}\right \left\ { \begin {array} {l}x=3ab5\\y=2a2b4\\z=a\\w=b\end {array} \right が一般解となる。22 任意の解が出るパターン 221 任意定数の決め方;23 解をもたないパターン 231 簡単な例;

第4回講義 基礎数学 数学入門

拡大係数行列の掃き出しにより連立方程式や逆行列を求める Youtube

大学数学 線形代数入門 連立方程式 掃き出し法 線形代数 Youtube

Http School Gifu Net Ed Jp Ena Hs Ssh H22ssh Sc3 Pdf

三元連立方程式 ２ 中２数学 Youtube

E Descubre Como Resolverlo En Qanda

行列式と行列 Determinant And Matrix

第１章 連立方程式

Http Polymer Chem Bio St Gunma U Ac Jp Renritu Pdf

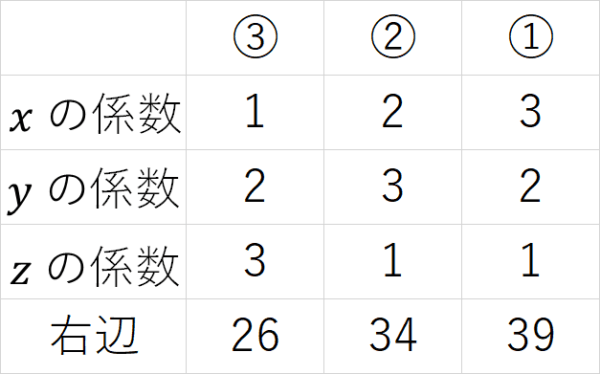
数学史５ ４ 紀元前の中国 連立方程式 Fukusukeの数学めも

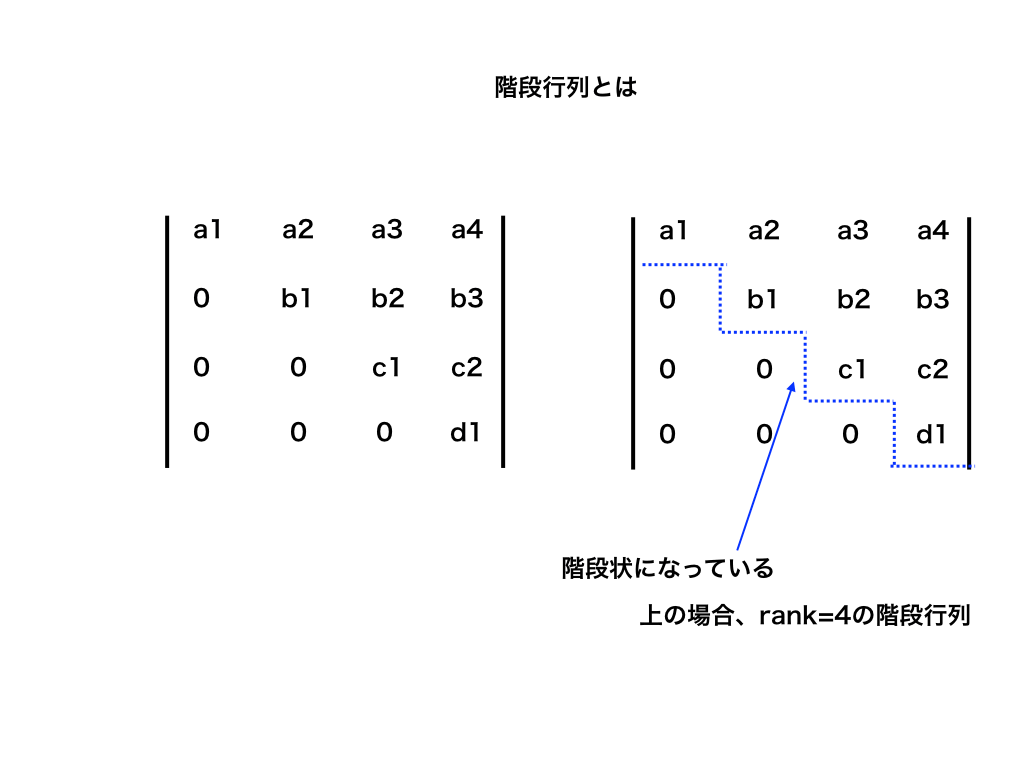
階段行列の作り方とランク 自由度の意味を連立方程式を解いて解説

連立一次方程式を掃き出し法で解く6つの例題 理数アラカルト

連立漸化式 ２ 行列で表す 怜悧玲瓏 高校数学を天空から俯瞰する

1

C言語で 3元1次連立方程式の解を求めるプログラムを作ったので Yahoo 知恵袋

連立方程式で３つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ

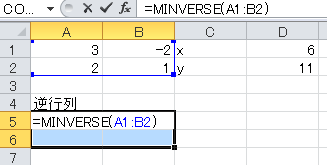
Excelを用いた連立方程式の解法

５ 連立一次方程式 Ppt Video Online Download

Pythonで線形代数 連立1次方程式を解く Watlab Python 信号処理 Ai

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

５ 連立一次方程式 Ppt Download

3元1次連立方程式に対するクラメールの解法

第１章 連立方程式

逆行列を求めて 実際に連立方程式を解いてみよう 線形代数を宇宙一わかりやすく解説してみるサイト

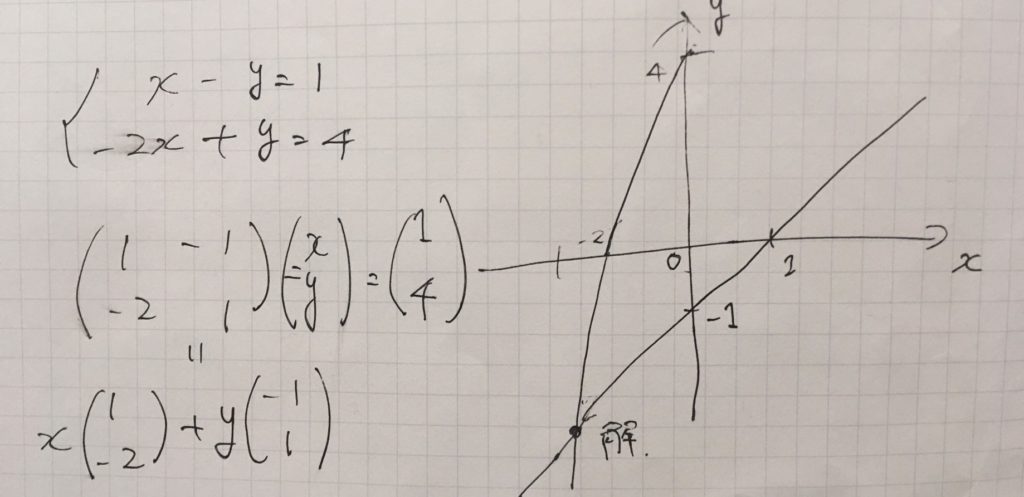
1次方程式を行列で解くメリット 方法 条件について 幾何学的に見る 趣味の大学数学

連立方程式の行列解

連立方程式編 解の条件 大学1年生もバッチリ分かる線形代数入門

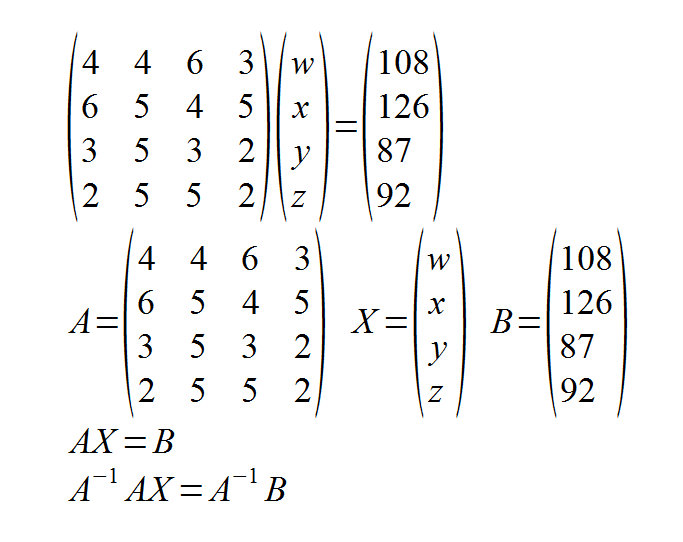
Excelで連立方程式を解く You Look Too Cool

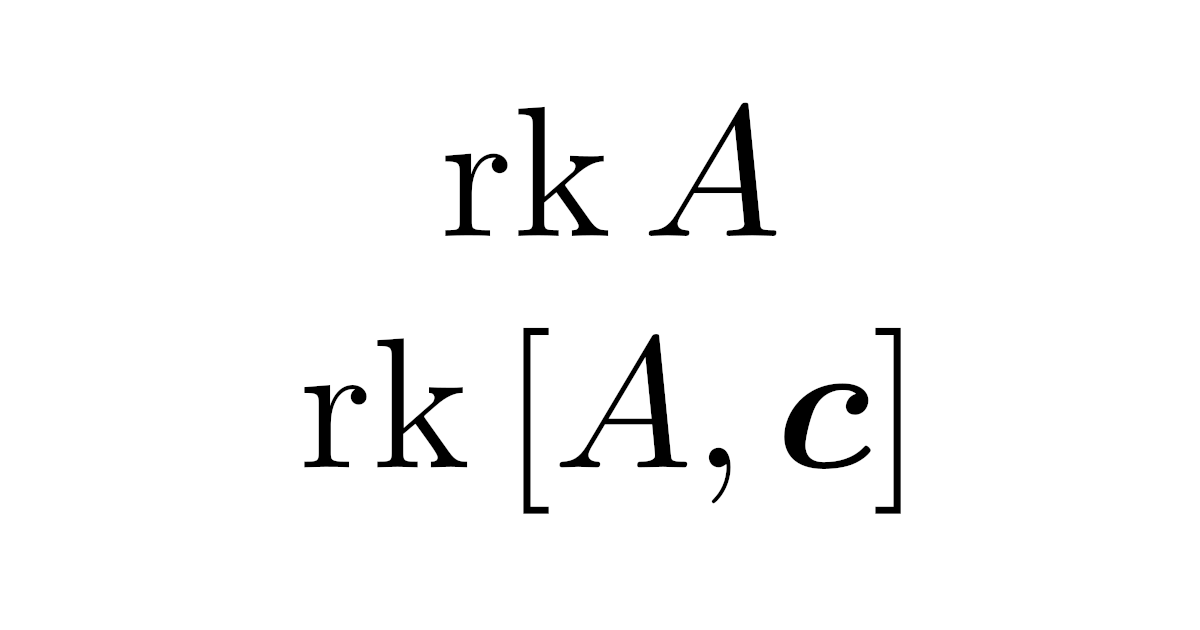
連立１次方程式が 解をもつ条件 と 解の自由度 の考え方

1

連立方程式から学ぶ行列 行列式 意味と計算の完全理解 数学のかんどころ 23 岡部 恒治 長谷川 愛美 村田 敏紀 飯高 茂 中村 滋 岡部 恒治 桑田 孝泰 本 通販 Amazon

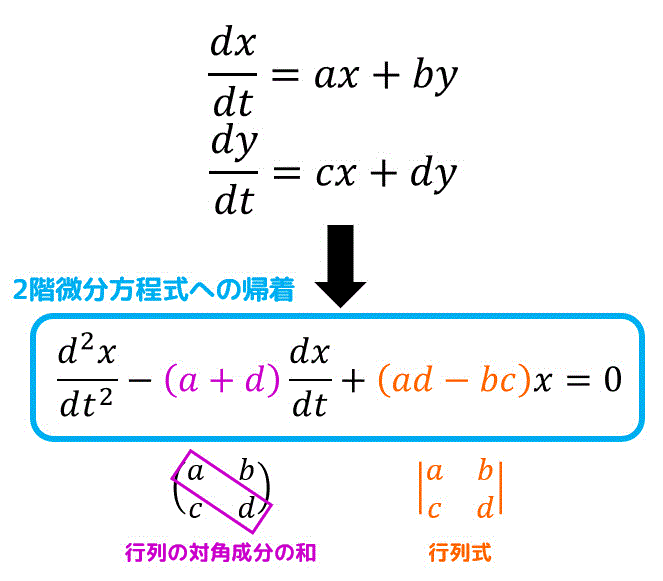
うさぎでもわかる微分方程式 Part10 連立微分方程式 2階微分方程式に帰着させて解くパターン 工業大学生ももやまのうさぎ塾

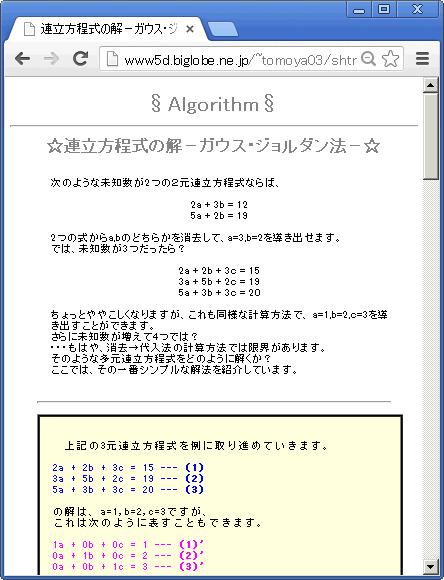
Pl Pgsql で多元連立方程式を解く 研究に使うポスグレ

1

行列式 方程式の解 Cramerの公式 余因数展開 Ppt Download

基礎数学演習ｉ

連立方程式の行列解

大学の数学 行列の加法 乗法と連立方程式への利用 ばけライフ

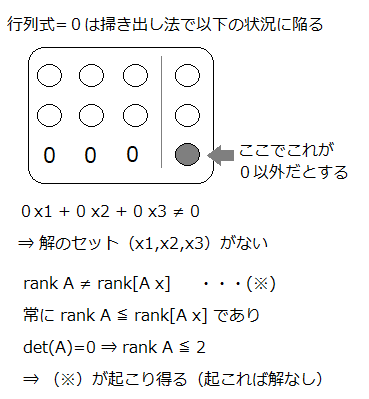
行列式が0だと解なしか不定解になるのに納得ができるまで 大学編入 文系の対策

文字が４つの連立方程式 Youtube

行列の連立方程式の問題で質問とお願いです Clear

連立一次方程式の解法について解説していきます Kaitalk

E Descubre Como Resolverlo En Qanda

連立方程式の行列解

第4回講義 基礎数学 数学入門

第１章 連立方程式

行列式 方程式の解 Cramerの公式 余因数展開 Ppt Download

５ 連立一次方程式 Ppt Video Online Download

Gauss Jordan の掃き出し法と 連立一次方程式の解き方 けんちょんの競プロ精進記録

Icu Hsuzuki Github Io Science Class Ns1b Lecnote 08 3 Linearalgebra Pdf

โน ตของ 連立方程式の解の判別式と行列式 行列式 1 ช น Clear

行列掃き出しの問題を解きましたが 間違いがありました どうしてこれが間違いでしょうか Clear

連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト

行列とは コトバンク

連立方程式の解 ガウス ジョルダン法

連立一次方程式を掃き出し法で解く6つの例題 理数アラカルト

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト

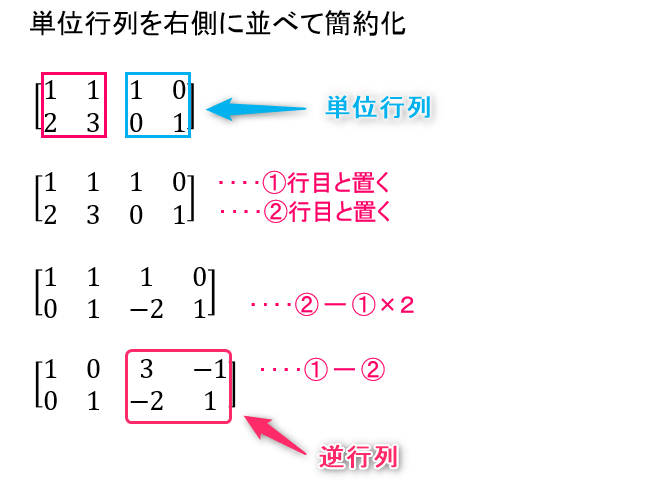
逆行列を求めて 実際に連立方程式を解いてみよう 線形代数を宇宙一わかりやすく解説してみるサイト

りんだろぐ Rindalog 行列で解く Systems Of Linear Equations

Gauss Jordan の掃き出し法と 連立一次方程式の解き方 けんちょんの競プロ精進記録

連立一次方程式の解の存在 北海道大学大学院の入試問題を例として考える 身勝手な主張

第１章 連立方程式

Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

第１章 連立方程式

行列と連立方程式について 以下の画像の問題です 1 は示すことが出 Okwave

５ 連立一次方程式 Ppt Video Online Download

連立方程式を行列で解く その仕組みをわかりやすく解説

行列式って何 大学1年生もバッチリ分かる線形代数入門

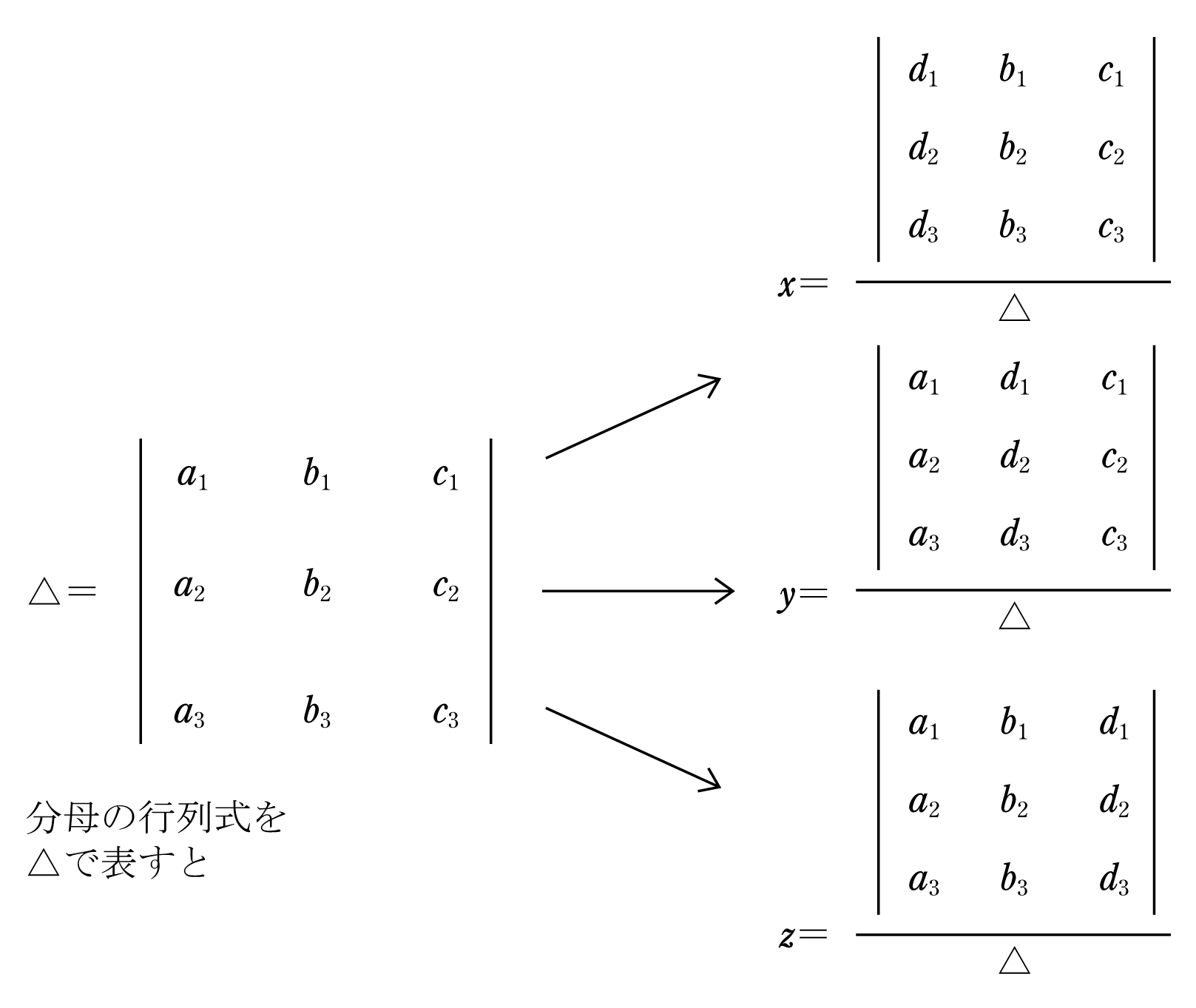
連立方程式と行列式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

書記が数学やるだけ 44 逆行列を求める 2 余因子行列 行列のランク 連立方程式 3 クラメールの公式 鈴華書記 Note

3元１次連立方程式から３次の行列式へ

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

連立１次方程式が 解をもつ条件 と 解の自由度 の考え方

四元連立方程式 ｈｏｍｅ

線形代数学 Ppt Video Online Laste Ned

連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点

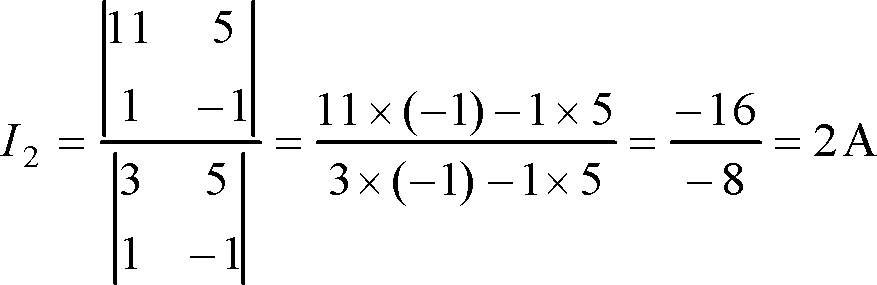
連立方程式と行列式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

連立一次方程式を掃き出し法で解く6つの例題 理数アラカルト

線形代数 解をもたないようなkの値 画像の連立１次方程式が解をもたないよ Okwave

クラメルで連立方程式 その２ 大学の数学 超入門シリーズ Youtube

連立一次方程式の解の存在 北海道大学大学院の入試問題を例として考える 身勝手な主張

Incoming Term: 連立方程式 3つ 行列,